[更新中]抛物线的一些性质与证明

形缺数时难入微，数缺形时少直观.

 本文是对抛物线的一些简单性质的整理与证明

 焦点弦的性质及证明

 交于两点A,B A(x1,y1),B(x2,y2)

$$y^{2} =2px \\ x_{1} x_{2}=\frac{p^{2} }{4} \\ y_{1} y_{2}=-p^{2}$$

证明

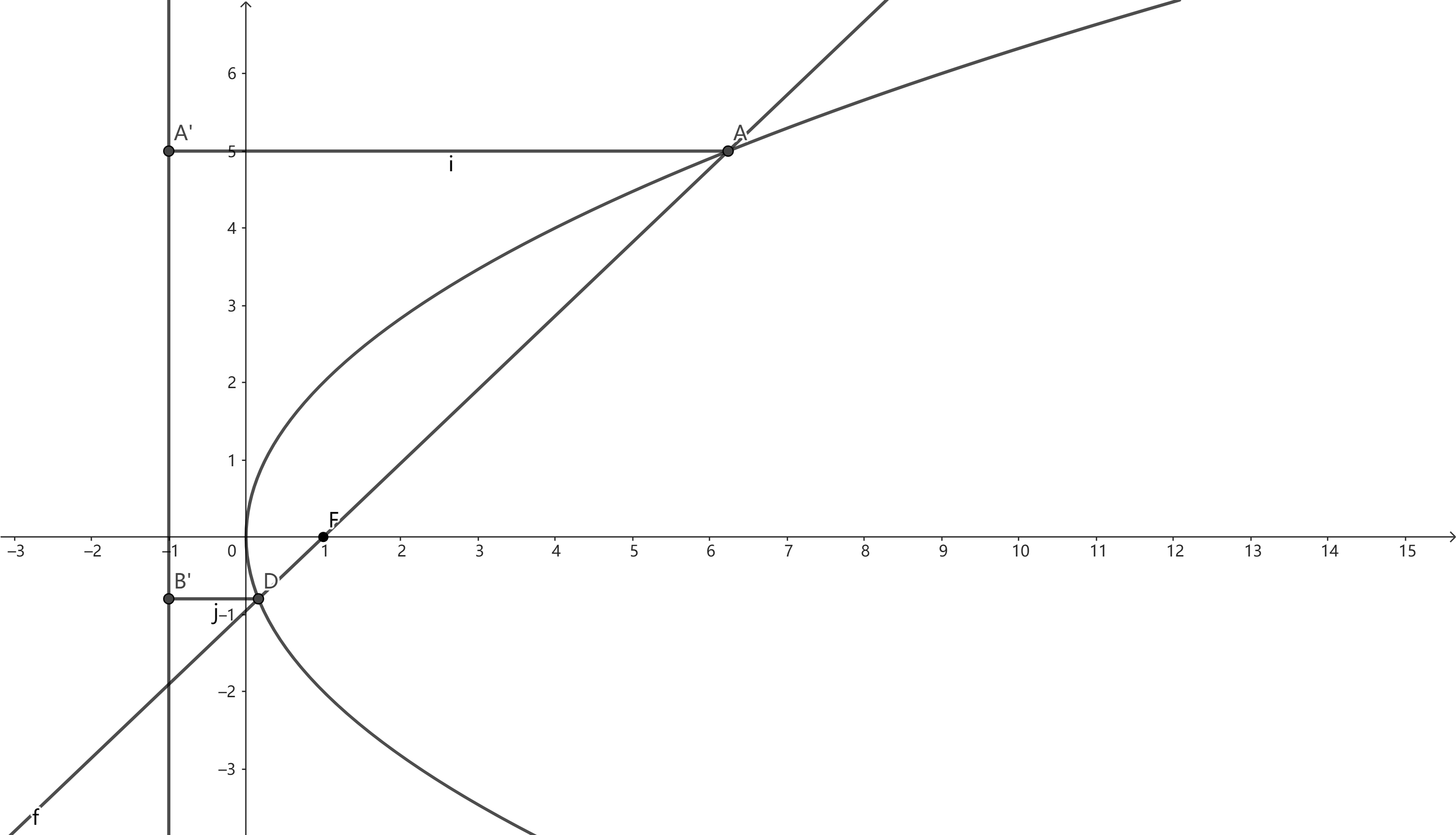
设

$$x=ty+\frac{p}{2}$$

联立方程：

$$\left\{ \begin{array}{l} y^{2} = 2px \\ x = ty + \frac{q}{2} \end{array} \right.$$

求解：

$$y^{2}=2p(ty+\frac{p}{2})=2pty+p^{2}$$

整理得:

$$y^{2}-2pty-p^{2}=0$$

由韦达定理可知：

$$y_{1}y_{2}=\frac{c}{a}=\frac{-p^{2}}{1}=-p^{2}$$

同理，如果我们设

$$y=k(x-\frac{p}{2})$$

联立求解可得

$$x_{1}x_{2}=\frac{p^{2}}{4}$$